執筆：中嶋（NIRO）
関係者：中嶋（NIRO）、迫田（県大学生）、永瀬（県大）
場所：兵庫県立大学・姫路工学キャンパス
日時：2023.12.27
メモ：歯車の数、計算などは現在確認中です（2024.01.07）。

・セイコーミュージアムでの同時代の実機の確認、新潟の笹川氏からのアドバイス聴取と当時の輸入品（モービエクロック）確認と、知識が深まってきたので、永瀬研究室を再訪し、実機を確認し、3Dモデルを作成した。
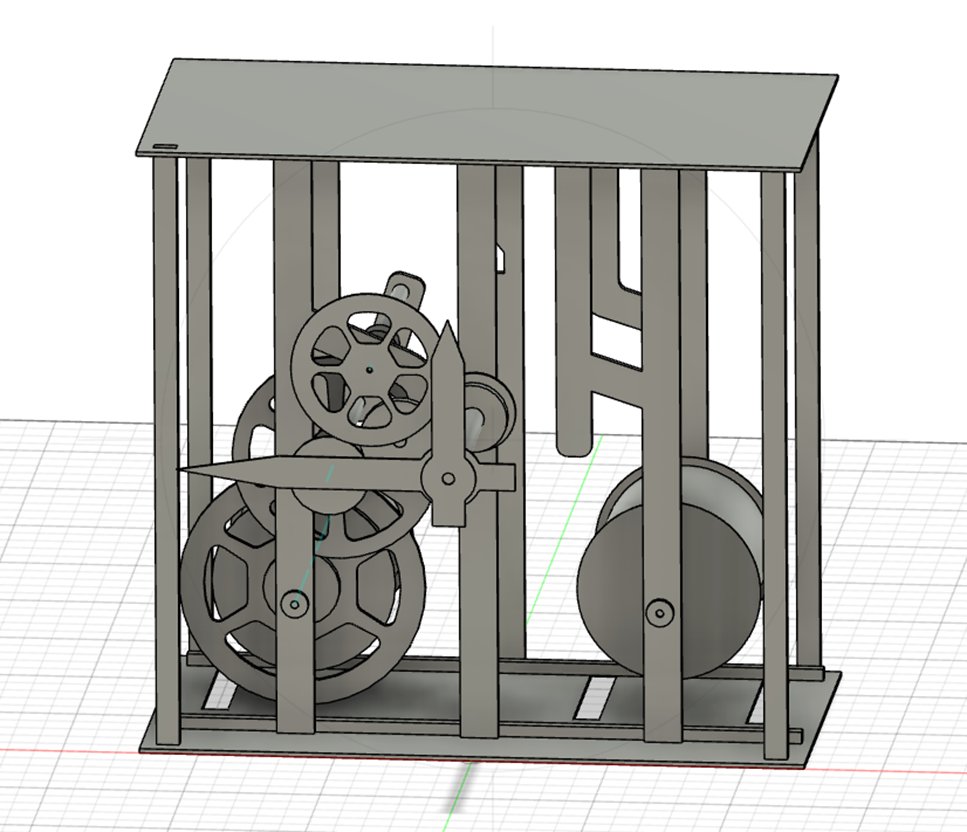
・以下に現状をモデル化したものを示す。歯車はピッチ円を円板として表し、歯の表現は行っていない。

・正面から見て左側が時間を表す部分、右側は時打ちの部分と思われる。右側はほとんど失われているので、左側のみ、注視した。２つの大きな滑車があるのは、分銅を下に垂らすロープを巻く滑車であり、こういう時計を分銅駆動と呼ぶ。一般的には分銅は、巻き上げられた状態から4日程度で下に下がる。出石1号機では、この滑車の回転を1段増速し、その後、同径の歯車3個で時計の針の軸に伝達する。ということは、伝達された針の軸の回転も遅いはずで、時針軸と考えられる。
・滑車軸の歯車はφ225、時針軸と同じ回転速度になる中間軸の歯車はφ37.3で225/37.3倍に中間軸は増速され、時針軸は720°/日＝30°/時で回転することになる。ということは、滑車軸は4.97°/時＝119.36°/日＝0.33回転/日と逆算される。
・滑車の径はφ152であるので、仮に分銅を吊り下げるロープの径をφ20とすると、ロープ中心の直径はφ172、滑車の長さは151mmなので、ロープは7巻となる。21日で7巻が開放され、分銅は3.8m下がる計算になる。分銅時計は標準的には4日、長いので8日に1回巻き上げると聞いているので、ロープ径がもう少し太かったかもしれない。滑車の下にある溝幅は24mmである。
・次に分針を予測する。中間軸には、使われていない大歯車がある。その大歯車の近くに使われていない穴がある。この穴に軸を通し、小歯車を回転させたと考える。この大歯車はφ190、小歯車はφ36である。すると、小歯車軸は時針軸の190/36倍で回転する。分針軸は360°/時、時針軸は30°/時なので、12倍の増速が必要である。小歯車軸を2.27倍の増速ができれば、分針軸を回転させられる。小歯車軸と分針軸の軸間距離は103.564mmである。この距離で2.27倍になる歯車の直径を計算する。小歯車軸に付く大歯車の径をd1、分針軸に付く小歯車の径をd2とすると、
d1/2＋d2/2＝103.564　　d1/d2＝2.27　　連立方程式を解くと、d2＝63.34、d1＝143.78となる。
・以上の推論から分針軸までを追加したモデルを以下に示す。